Modeling of self-healing materials based on continuum damage healing mechanics
Current area of research work
I am currently working on constitutive modelling of self-healing materials using continuum damage-healing mechanics. The primary objective of my work is to mathematically model the behavior and understand the mechanism of self-healing in materials under different loading conditions.
What is self-healing in materials?
Self-healing is the ability of certain materials to recover the degradation in material properties caused by damage. The process of self-healing delays failure and improves the life cycle of materials, which is crucial in structural design.
The nature of self-healing varies from one material to another. Self-healing is achieved in some materials by addition of microcapsules containing monomers, which break open in the presence of a crack and mix with a pre-dispersed catalyst to heal the crack[1][2]. The mechanical properties of damaged material can also be recovered at elevated temperatures and during rest periods in some natural materials[3].
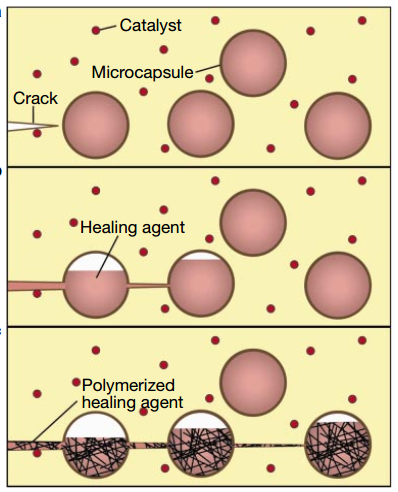
Figure 1: Healing by addition of microcapsules[1]
How are self-healing materials modelled?
Modelling of self-healing materials has been of great interest in the last two decades especially using continuum damage mechanics (CDM). Continuum damage mechanics deals with meso-scale modeling of the degradation of material upon loading until the formation of a macro-crack.
In continuum damage mechanics, the representative volume element which has undergone damage upon loading is defined as the damaged (current) configuration. Another configuration with all the damaged area removed from the current configuration is defined as the effective configuration. The effective configuration has only the undamaged material.
Different principles such as the principle of strain equivalence, principle of strain energy equivalence are employed to establish a relation between the stiffness of the configurations, where the strain or strain energy in both the configurations are hypothesised to be equal.
A part of the damaged area undergoes healing in self-healing materials. An additional configuration called as the healing configuration is thus introduced where the damaged area that has not undergone healing is removed from the current configuration (Figure 2)
Damage and healing variables are defined to quantify the fraction of damaged and healed areas in the representative volume element. An effective damage density variable is also defined which captures both damage and healing. A relation is established between the stresses in current and healing configurations based on the principle of mechanical equivalence. Damage and healing evolution equations are utilised to study the growth of damage and healing in the self-healing materials. A consistent thermodynamic framework is thus developed to study the variation in mechanical properties of self-healing materials.

Figure 2: Schematic representation of the current, healing and effective configurations[4]
Novel elastic-damage healing model
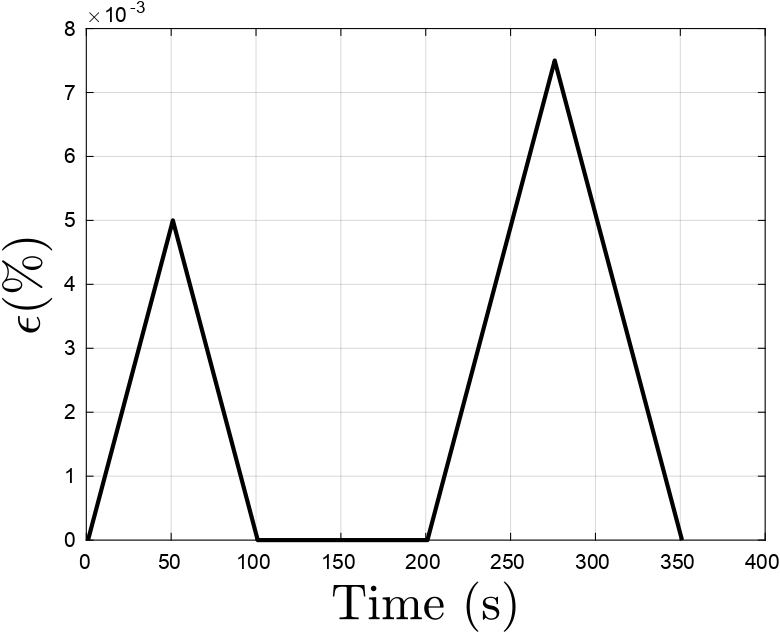
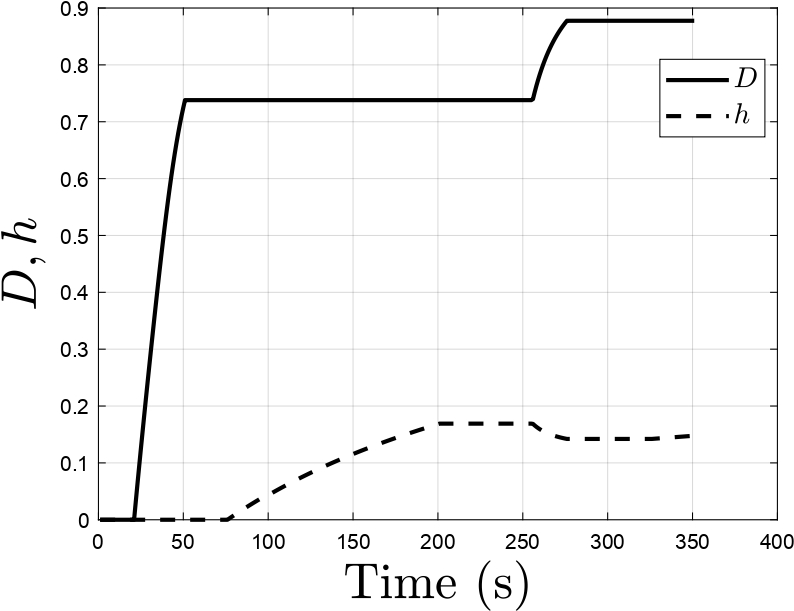
An elastic damage-healing model has been proposed to obtain the constitutive response of materials that undergo self-healing during unloading and rest periods causing the damage surfaces to wet each other and partially recover their strength. The molecules diffuse from one surface of the microcrack to the other. The diffused molecules randomize reaching the properties of original undamaged material. Separate damage and healing evolution laws are defined which are coupled through the healing configuration. Figures 3-6 show the response obtained using the proposed damage-healing model for two dif- ferent strain inputs. The stress-strain response, evolution of damage, healing and effective damage density variables have also been plotted. Damage variable monotonically increases whereas the effective damage density variable does not monotonically increase due to the presence of healing. The stress-strain response show a recovery in stiffness during unloading and after a rest period indicating the occurrence of healing. This is seen as an increase in stiffness of the material during reloading.
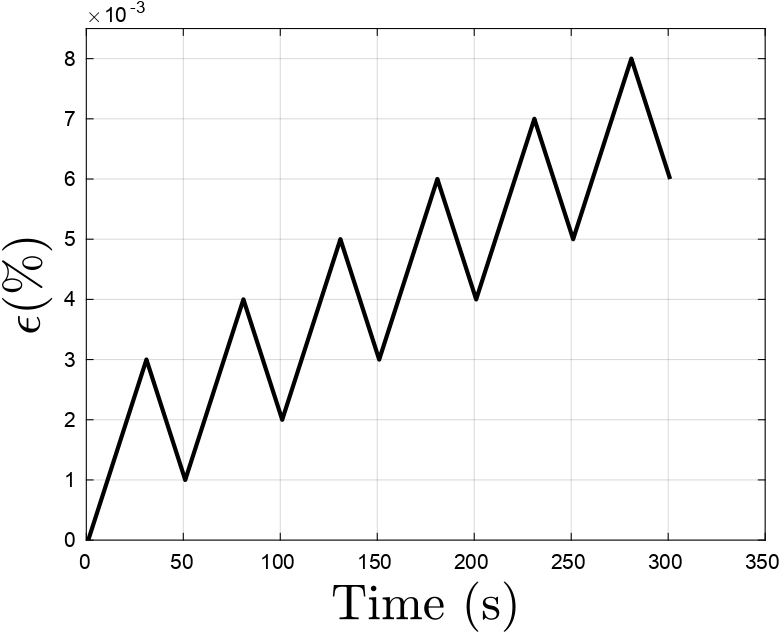
(a)
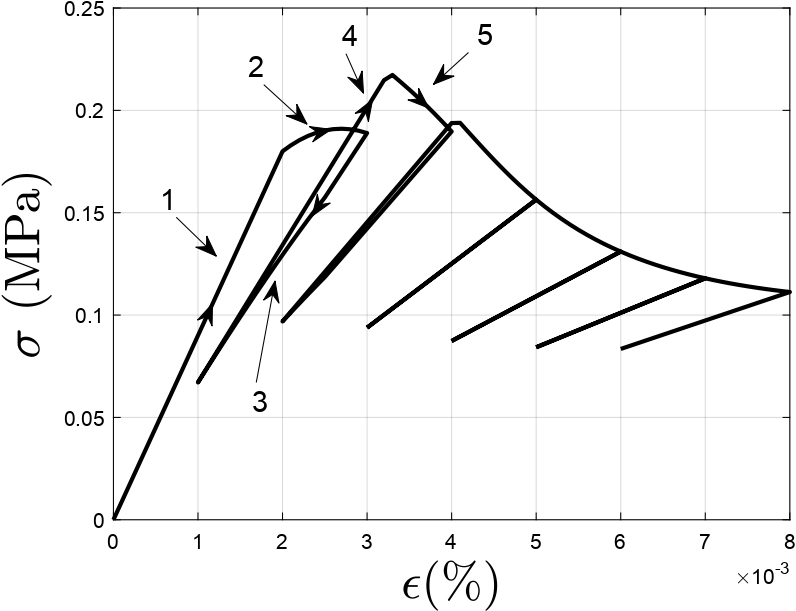
(b)
Figure 3: Plots of (a) strain input with partial unloading-reloading, (b) stress vs strain response[4]

(a)
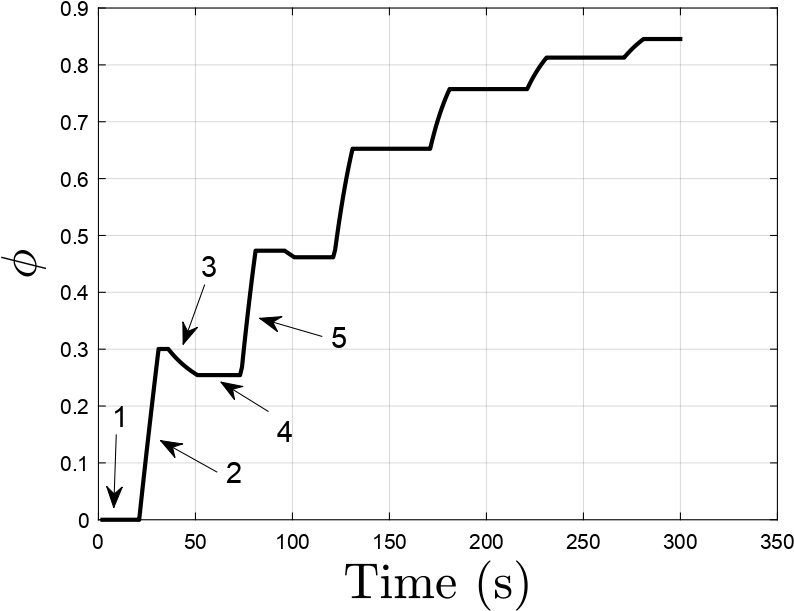
(b)
Figure 4: Plots of (a) variation of damage and healing variables with respect to time, (b) variation of effective damage density with time[4]
(a)

(b)
Figure 5: Plots of (a) strain input with equal loading-unloading with rest period, (b) stress vs strain response[4]
(a)
(b)
Figure 6: Plots of (a) variation of damage and healing variables with respect to time, (b) variation of effective damage density with time[4]
References
- [1] Scott R White, Nancy R Sottos, Philippe H Geubelle, Jeffrey S Moore, Michael R Kessler, SR Sriram, Eric N Brown, and S Viswanathan. Autonomic healing of polymer composites.Nature, 409(6822):794–797, 2001.
- [2] Swapan Kumar Ghosh.Self-healing materials: fundamentals, design strategies, and applications.Wiley Online Library, 2009.
- [3] Rashid K Abu Al-Rub, Masoud K Darabi, Dallas N Little, and Eyad A Masad. A micro-damage healing model that improves prediction of fatigue life in asphalt mixes.International Journal of Engineering Science, 48(11):966–990, 2010.
- [4] Harini Subramanian and Shantanu S Mulay. Continuum damage–healing-based constitutive modelling for self-healing materials: application to one-dimensional cyclic loading cases.International Journal of Advances in Engineering Sciences and Applied Mathematics, 12(1):3–18, 2020.